寿命の検討

ボールねじの寿命

ボールねじが外部荷重を受けて運動する場合、転動面やボールにはたえず繰り返し応力が作用し、限界に達すると、転動面は疲れ破損し、表面の一部がうろこ状にはく離します。これをフレーキングと呼んでいます。ボールねじの寿命とは、転動面あるいはボールのいずれかに材料の転がり疲れによる最初のフレーキングが発生するまでの総回転数をいいます。
ボールねじの寿命は、同じように製作されたものを同一運動条件で使用しても、バラツキがあります。このためボールねじの寿命を求める目安として、つぎのように定義された定格寿命を使用します。
定格寿命とは、一群の同じボールねじを同じ条件で個々に運動させたとき、そのうちの90%がフレーキング(金属表面のうろこ状のはく離)をおこすことなく到達できる総回転数をいいます。

定格寿命計算

ボールねじの定格寿命は基本動定格荷重(Ca)と、負荷軸方向荷重から(32)式により求められます。

定格寿命の算出

定格寿命(L₁₀)は基本動定格荷重(Ca)とボールねじに負荷する軸方向荷重(Fa)から次式により求められます。

使用条件を考慮した定格寿命の算出

実際の使用では稼動中に振動や衝撃を伴う場合が多いため、ボールねじへの作用荷重の変動が考えられ正確に把握することは容易ではありません。これらの条件を考慮すると、次式(32-2)により使用条件を考慮した定格寿命(L_10m)を算出することができます。

表19 荷重係数(f_W)

振動・衝撃	速度(V)	f_W
微	微速の場合 V≦0.25m/s	1〜1.2
小	低速の場合 0.25<V≦1m/s	1.2〜1.5
中	中速の場合 1<V≦2m/s	1.5〜2
大	高速の場合 V>2m/s	2〜3.5

※基本動定格荷重(Ca)は、ボールねじが軸方向荷重を受けて運動する場合の寿命の算出に使用します。基本動定格荷重(Ca)とは、一群の同じボールねじを個々に運動させたとき、定格寿命がL=10⁶revとなるような、軸方向に作用する方向と大きさの変動しない荷重をいいます。(基本動定格荷重(Ca)は、各形番の寸法表中に記載してあります。)
※定格寿命は、良好な潤滑が確保でき、理想的な取付条件で組立てることを前提に荷重計算を行い算出しております。取付部材の精度および変形によっては寿命に影響を与える恐れがあります。

寿命時間

毎分回転数が求められている場合、定格寿命(L₁₀)から(33)式により寿命時間が求められます。

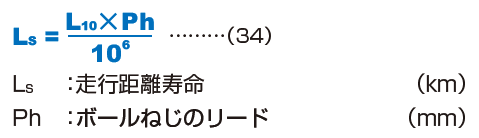
走行距離寿命

定格寿命(L₁₀)とボールねじのリードから(34)式により走行距離寿命が求められます。

予圧を考慮した負荷荷重と寿命

ボールねじナットに予圧(中予圧)をかけて使用する場合、ボールねじナットにあらかじめ内部荷重を作用させているので、その予圧荷重を考慮して寿命計算を行う必要があります。なお、予圧荷重は形番を設定のうえ、THKにお問い合わせください。

軸方向平均荷重

ボールねじに作用する軸方向荷重が変動する場合は、軸方向平均荷重を求めて寿命計算する必要があります。
軸方向平均荷重(F_m)とは、変動荷重条件における寿命と等しい寿命となるような一定荷重をいいます。
荷重が段階的に変化する場合は、次式により軸方向平均荷重は求められます。

距離の代わりに回転数と時間で求める場合は、次式で距離を求めて軸方向平均荷重を算出してください。

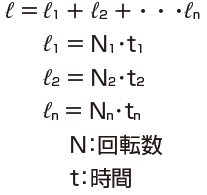
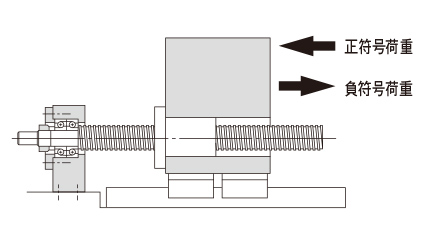
荷重負荷の符号が変化する場合

変動荷重の符号がすべて同一の場合、(35)の式で問題ないのですが、変動荷重の符号が動作により変化する場合には、荷重の方向を考慮して、正符号荷重の軸方向平均荷重、負符号荷重の軸方向平均荷重を算出します。(正符号負荷の軸方向平均荷重を計算する場合、負符号荷重をゼロとして計算します。)そこで2種類の軸方向平均荷重の大きい方を寿命計算時の軸方向平均荷重とします。
例) 荷重条件で軸方向平均荷重を算出すると、以下となります。

動作No.	変動荷重Fa_n(N)	走行距離ℓ_n(mm)
No.1	10	10
No.2	50	50
No.3	-40	10
No.4	-10	70

※変動荷重、走行距離の添字は動作No.を示します。

正符号荷重の軸方向平均荷重

※正符号荷重の軸方向平均荷重算出のため、Fa₃、Fa₄はゼロとして計算します。

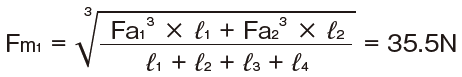
負符号荷重の軸方向平均荷重

※負符号荷重の軸方向平均荷重算出のため、Fa₁、Fa₂はゼロとして計算します。

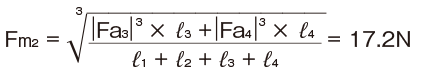
以上より正符号荷重の軸方向平均荷重(F_m1)を寿命計算時の軸方向平均荷重(F_m)として採用します。